Tam arama, neredeyse her algoritma probleminde kullanılan bir metottur. Buradaki fikir, kaba kuvvet (brute force) kullanarak bütün olası çözümleri oluşturup sonrasında probleme göre aralarından en iyi çözümü bulmak veya bütün çözümleri saymaktır. Tam arama, bütün çözümler denenebiliyorsa işe yarar bir tekniktir çünkü bu aramayı koda dökmek kolaydır ve aynı zamanda her zaman doğru çözümü bulur. Eğer tam arama soru için çok yavaş kalıyorsa, açgözlü (greedy) algoritmalar veya dinamik programlama gibi başka yöntemler gerekebilir.
5.1 Alt küme Oluşturmak (Generating Subsets)
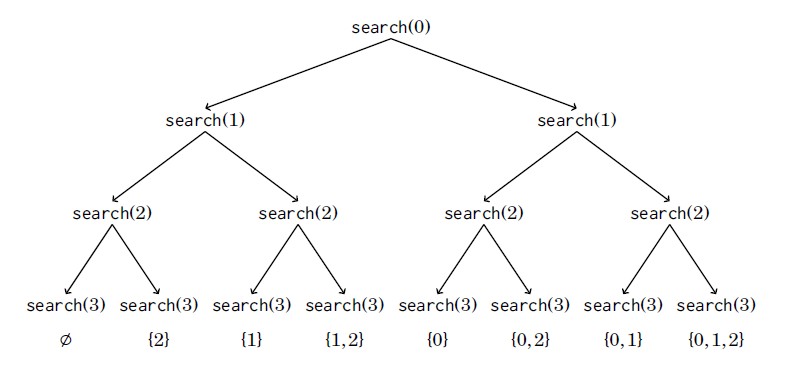
n elemanlı bir kümenin bütün alt kümelerini oluşturmak için iki yaygın yöntem vardır: özyineleme (recursion) veya bit maskeleme (bitmasking).
Yöntem 1: Özyineleme (Recursion)
Bütün alt kümeleri oluşturmanın şık yollarından biri özyinelemedir. Aşağıdaki search fonksiyonu {0, 1, ..., n-1} kümesinin alt kümelerini oluşturur.
vector<int> subset;
void search(int k) {
if (k == n) {
// alt kümeyi işle
} else {
// k elemanını alt kümeye dahil etme
search(k + 1);
// k elemanını alt kümeye dahil et
subset.push_back(k);
search(k + 1);
subset.pop_back();
}
}
Yöntem 2: Bit Maskeleme (Bitmasking)
n elemanlı bir kümenin her alt kümesi, n bitten oluşan bir tam sayı (bitmask) ile temsil edilebilir. Sayıdaki 1 olan bitler, o pozisyondaki elemanın alt kümede olduğunu gösterir.
for (int b = 0; b < (1 << n); b++) {
vector<int> subset;
for (int i = 0; i < n; i++) {
if (b & (1 << i)) {
subset.push_back(i);
}
}
// alt kümeyi işle
}
5.2 Permütasyon Oluşturmak (Generating Permutations)
Yöntem 1: Özyineleme (Recursion)
Permütasyonlar da özyineleme kullanılarak oluşturulabilir. Aşağıdaki kod, {0, 1, ..., n-1} kümesinin tüm permütasyonlarını bulur.
vector<int> permutation;
bool chosen[n+1];
void search() {
if (permutation.size() == n) {
// permütasyonu işle
} else {
for (int i = 0; i < n; i++) {
if (chosen[i]) continue;
chosen[i] = true;
permutation.push_back(i);
search();
chosen[i] = false;
permutation.pop_back();
}
}
}
Yöntem 2: C++ next_permutation
C++ standart kütüphanesi, bir dizinin bir sonraki leksikografik permütasyonunu oluşturan next_permutation fonksiyonunu içerir.
vector<int> p;
for (int i = 0; i < n; i++) {
p.push_back(i);
}
do {
// permütasyonu işle
} while (next_permutation(p.begin(), p.end()));
5.3 Geri İzleme (Backtracking)
Geri izleme, boş bir çözümle başlayıp çözümü adım adım büyüten bir tam arama tekniğidir. Arama, çözüme ulaşmayan yolları terk ederek (geri izleyerek) ilerler.
Klasik bir örnek n-Vezir Problemi‘dir: n x n bir satranç tahtasına n veziri, birbirlerini tehdit etmeyecek şekilde yerleştirmek.
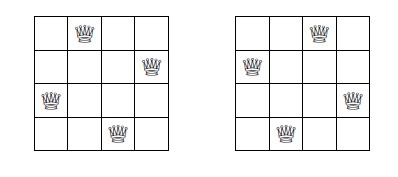
Bu problem, her satıra sırayla bir vezir koyarak ve her yeni vezirin öncekileri tehdit etmediğinden emin olarak geri izleme ile çözülebilir.
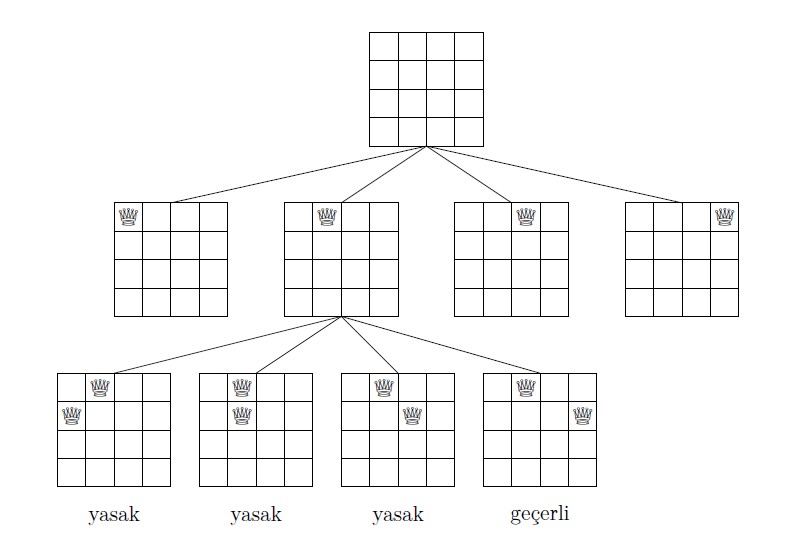
5.4 Aramayı Budama (Pruning The Search)
Arama ağacını budayarak geri izleme optimize edilebilir. Buradaki fikir, yarı-çözümün tam bir çözüme ulaşamayacağı anlaşıldığı anda o arama dalını terk etmektir. Bu optimizasyonlar, aramanın verimliliğini ciddi derecede artırabilir.
Örneğin, n x n bir tahtada sol üst köşeden sağ alt köşeye her kareden tam bir kez geçerek yol bulma probleminde, aşağıdaki gibi optimizasyonlar yapılabilir:
- Simetri: Sadece aşağı veya sağa giderek başlayıp sonucu ikiyle çarpmak.
- Erken Varış: Tüm kareler gezilmeden hedefe varıldıysa yolu geçersiz saymak.
- Bölünme: Yol bir duvara ulaştığında, eğer sola ve sağa gidebiliyorsa tahtayı ikiye böler ve tüm kareleri gezmek imkansız hale gelir. Bu durumda arama dalı budanır.
Bu tür küçük optimizasyonlar, arama süresini yüzlerce kat hızlandırabilir.
5.5 Ortada Buluşmak (Meet in the middle)
Ortada buluşmak (meet-in-the-middle), arama uzayını iki eşit parçaya bölerek çalışan bir tekniktir1. Her parça için ayrı bir arama yapılır ve sonda bu aramaların sonuçları birleştirilir. Genelde, $O(2^n)$ olan bir zaman karmaşıklığını $O(2^{n/2})$’ye indirebilir.
Örnek problem: n elemanlı bir kümede, toplamları x olan bir alt küme bulmak.
- Kümeyi
n/2elemanlı A ve B olmak üzere ikiye ayır. - A kümesinin tüm alt küme toplamlarını hesapla ve bir
S_Alistesine kaydet. - B kümesinin tüm alt küme toplamlarını hesapla ve bir
S_Blistesine kaydet. S_A‘dan hers_atoplamı için,S_B‘dex - s_adeğerinin olup olmadığını kontrol et.
Bu yaklaşım, $O(2^n)$ yerine $O(2^{n/2})$ zamanda çalışır çünkü her iki yarım için de arama uzayı önemli ölçüde küçülür.
-
Bu algoritma, E. Horowitz ve S. Sahni tarafından 1974’te bulunmuştur. ↩
Yorumlar