Rekabetçi Programcı Sıralama

Sıralama, temel algoritma sorularından biridir. Çoğu algoritmanın içeriğinde, veriyi sıralı halde işlemek daha kolay olduğu için sıralama bulunur. Örneğin “Bu dizide birbiriyle aynı iki eleman var mı?” sorusu sıralamayla çok kolay bir şekilde çözülebilir. Eğer dizi birbiriyle aynı iki eleman içeriyorsa, dizi sıralandıktan sonra bu elemanlar ardışık olacaktır.

Verimli çalışan sıralama algoritmaları $O(n \log n)$ zamanda çalışır ve genelde içeriğinde sıralama bulunan algoritmalar da bu zaman karmaşıklığına sahiptir.

3.1 Sıralama Teorisi

Temel sıralama problemi şöyledir: n elemana sahip bir diziyi artan sırada sıralayın. Örneğin [1, 3, 8, 2, 9, 2, 5, 6] dizisi sıralandıktan sonra [1, 2, 2, 3, 5, 6, 8, 9] haline dönüşür.

$O(n^2)$ Algoritmalar

Basit dizi sıralama algoritmaları $O(n^2)$ zamanda çalışır. Bu algoritmalar kısa olup genelde iki for döngüsüyle çalışır. Çok bilinen $O(n^2)$ algoritmalarından biri olan kabarcık sıralaması (bubble sort), dizideki elemanların değerlerine göre “kabarcık” gibi yer değiştirmesiyle çalışır.

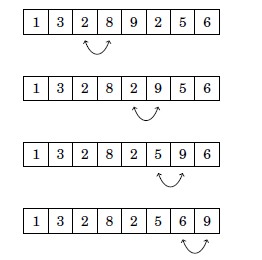
Kabarcık sıralaması n defa tur atar. Her turda, algoritma sıraya uymayan iki ardışık eleman bulduğunda yerlerini değiştirir.

for (int i = 0; i < n; i++) {
  for (int j = 0; j < n - 1; j++) {
    if (array[j] > array[j+1]) {
      swap(array[j], array[j+1]);
    }
  }
}

Ters Elemanlar (Inversions)

Bir dizide a < b iken array[a] > array[b] olması durumuna ters eleman (inversion) denir. Dizide herhangi bir ters eleman durumu kalmayınca dizi sıralanmış olur. En kötü durumda (dizi tersten sıralıysa) ters eleman sayısı $\frac{n(n-1)}{2} = O(n^2)$ olur. Sadece ardışık elemanları değiştiren algoritmalar her adımda en fazla bir ters eleman durumunu düzeltebildiği için zaman karmaşıklıkları en az $O(n^2)$’dir.

$O(n \log n)$ Algoritmalar

Bir diziyi, sadece ardışık eleman değiştirmeye bağlı kalmayarak $O(n \log n)$’lık algoritmalarla sıralayabiliriz. Bu tip algoritmalardan biri özyinelemeye (recursion) dayalı birleştirme sıralamasıdır (merge sort)¹.

Birleştirme sıralaması array[a...b] alt dizisini aşağıdaki gibi sıralar:

Eğer a == b ise, alt dizi zaten sıralıdır.
Orta elemanın pozisyonunu hesapla: $k = \lfloor(a+b)/2\rfloor$.
Özyinelemeli bir şekilde array[a...k] alt dizisini sırala.
Özyinelemeli bir şekilde array[k+1...b] alt dizisini sırala.
Sıralı alt dizileri birleştirerek array[a...b]‘yi oluştur.

Sıralama Alt Sınırı (Lower Bound)

Elemanları sadece birbiriyle karşılaştırarak çalışan sıralama algoritmaları için zaman karmaşıklığı alt sınırı $O(n \log n)$’dir. Bunun nedeni, n elemanın n! tane olası permütasyonu olması ve her karşılaştırmanın bu olasılıkları en fazla yarıya indirmesidir. Bu durumu ayırt etmek için en az $\log_2(n!) \approx O(n \log n)$ karşılaştırma gerekir.

Sayarak Sıralama (Counting Sort)

Eğer dizideki her elemanın değerinin $0…c$ arasında olduğu biliniyorsa ve $c=O(n)$ ise, sayarak sıralama (counting sort) ile diziyi $O(n)$ zamanda sıralayabiliriz. Bu algoritma, her elemanın dizide kaç kez geçtiğini sayan bir frekans dizisi oluşturur ve bu diziyi kullanarak sıralı diziyi oluşturur.

3.2 C++ Dilinde Sıralama

Yarışmalarda kendi sıralama algoritmanızı yazmak yerine standart kütüphanelerdeki hazır fonksiyonları kullanmak daha pratiktir. C++’daki sort fonksiyonu verimli bir şekilde çalışır.

Vector sıralama:

vector<int> v = {4, 2, 5, 3, 5, 8, 3};
sort(v.begin(), v.end()); // v becomes {2, 3, 3, 4, 5, 5, 8}

Dizi (array) sıralama:

int a[] = {4, 2, 5, 3, 5, 8, 3};
int n = 7;
sort(a, a + n);

String sıralama:

string s = "monkey";
sort(s.begin(), s.end()); // s becomes "ekmnoy"

Karşılaştırma İşlemleri

sort fonksiyonu, pair ve tuple gibi yapıları da sıralayabilir. Sıralama önce ilk elemana göre, eşitlik durumunda ikinci elemana göre vb. yapılır.

Kendi tanımladığınız yapılar (struct) için operator< fonksiyonunu tanımlamanız gerekir:

struct P {
  int x, y;
  bool operator<(const P &p) {
    if (x != p.x) return x < p.x;
    else return y < p.y;
  }
};

Alternatif olarak sort fonksiyonuna üçüncü bir argüman olarak bir karşılaştırma fonksiyonu da verebilirsiniz.

3.3 İkili Arama Algoritması (Binary Search)

Eğer bir dizi sıralıysa, içinde bir elemanı aramak için O(n)‘lik lineer arama yerine O(log n)‘de çalışan ikili arama (binary search) kullanılabilir. İkili arama, arama aralığını her adımda ikiye bölerek çalışır.

Yöntem 1: Aralık Küçültme

int a = 0, b = n - 1;
while (a <= b) {
  int k = (a + b) / 2;
  if (array[k] == x) {
    // bulundu
  }
  if (array[k] > x) b = k - 1;
  else a = k + 1;
}

Yöntem 2: Zıplamalı Arama

int k = 0;
for (int b = n / 2; b >= 1; b /= 2) {
  while (k + b < n && array[k + b] <= x) {
    k += b;
  }
}
if (array[k] == x) {
  // bulundu
}

C++ Fonksiyonları

C++ standart kütüphanesi, sıralı diziler üzerinde logaritmik zamanda çalışan hazır ikili arama fonksiyonları sunar:

lower_bound: Değeri en az x olan ilk elemanın işaretçisini (pointer/iterator) döner.
upper_bound: Değeri x‘ten büyük olan ilk elemanın işaretçisini döner.
equal_range: Yukarıdaki iki işaretçiyi bir çift olarak döner.

Bu fonksiyonları kullanarak bir elemanın dizide olup olmadığını kontrol edebilir veya kaç adet bulunduğunu sayabilirsiniz.

En Küçük Çözümü Bulmak

İkili arama, belirli bir k değerinden sonra true olan bir ok(x) fonksiyonu için bu en küçük k değerini bulmak amacıyla da kullanılabilir. Bu, “cevaba ikili arama” (binary search on the answer) olarak bilinen yaygın bir tekniktir.

Birleştirme sıralaması J. von Neumann tarafından 1945 tarihinde icat edilmiştir. ↩

sıralama c programlama algoritma olimpiyat karmaşıklık yarışma kabarcık sıralaması ters elemanlar ikili arama kodlama matematik kitap