Python Programlama Ders 6. Döngüler - while döngüsü

Yineleme (Döngü)

Bilgisayarlar sıklıkla tekrarlayan görevleri otomatikleştirmek için kullanılmaktadır. Aynı veya benzer görevleri hatasız bir şekilde tekrarlama işlemi bilgisayarların iyi yaptığı, insanların ise zorlandığı bir şeydir.

Bir komutlar kümesinin tekrar tekrar yürütülmesi işlemine yineleme (iteration) adı verilir. Yineleme çok yaygın olduğu için, Python bunu kolaylaştırmak için birkaç özellik sağlar. Daha önceki bölümlerde for deyimini gördük. for deyimi en sık kullanacağınız döngü komutu olacaktır. Fakat bu bölümde while deyimine bakacağız. Bu, azıcık farklı durumlarda yineleme yapmanın başka değişik yoludur.

6.1 Birden fazla atama

Keşfetmiş olabileceğiniz gibi, aynı değişkene birden fazla atama yapılması geçerli bir yöntemdir. Yeni bir atama varolan değişkeninin yeni bir değeri temsil etmesini sağlar (ve önceki-eski değeri temsiliyetini ortadan kaldırır).

  
bruce = 5
print(bruce,end=" ")
bruce = 7
print(bruce)

Yukarıdaki programın çıktısı 5 7 şeklindedir, çünkü bruce değişkenini ilk görüntülememizden önce,değeri 5’tir, ve daha sonra ikinci görüntülemede 7 olmaktadır. İlk print cümlesindeki bruce değişkeninden sonra gelen end parametresi yeni bir satır yaratılmasını engeller, bu yüzden iki print cümlesinin çıktısı da aynı satırdadır. print() fonksiyonu hakkında daha detaylı kullanımı şu konuda bulabilirsiniz print fonksiyonu

Aşağıda birden fazla atama‘nın bir durum diyagramında nasıl gözüktüğünü inceleyebilirsiniz:

Birden fazla atamalarda, atama işlemi ve eşitlik cümlesini birbirinden ayırmak oldukça önemlidir. Çünkü Python eşit işaretini (=) atama için kullanmaktadır. a=b şeklindeki bir cümleyi eşitlik olarak algılamak çekici gelebilir, ancak bu ifadenin eşitlik ifadesi olmadığı unutulmamalıdır!

İlk olarak, eşitlik simetriktir ve atama değildir. Örneğin, matematikte, eğer a=7 ise 7=a’dır. Python’da a = 7 cümlesi geçerli bir ifade olmasına rağmen, 7 = a geçerli bir ifade değildir.

Ayrıca, matematikte eşitlik cümlesi her zaman doğrudur. Eğer şimdi a = b ise, daha sonra da a her zaman b’ye eşit olacaktır. Python’da, bir atama işleci iki değişkeni eşitleyebilir ancak sürekli bu şekilde kalmaları gerekli değil:

  
a = 5
b = a    # a ve b şimdi eşitler
a = 3    # a ve b artık eşit değiller

Üçüncü satır a değişkeninin değerini değiştirir ama b değişkeninin değerini değiştirmez, bu yüzden o satırın işletilmesinden sonra artık eşit değillerdir. (Bazı programlama dillerinde, karmaşayı önlemek için atama işleminde farklı bir işaret, <- veya := gibi, karmaşayı önlemek için kullanılmaktadır)

6.2 Değişkenleri güncelleme

Birden fazla atamanın en sık biçimi güncellemedir, bir değişkenin değerini eskisine bağlı olarak değiştirmektir.

  
x = x + 1

Bu ifadenin anlamı x’in değerini al, bu değere 1 ekle ve x’i yeni değerle güncelle

Eğer varolmayan bir değişkeni güncellemeye çalışırsanız, bir hata oluşur, çünkü Python atama işleminde öncelikle sağ taraftaki deyimi değerlendirdikten sonra oluşan sonucu sol taraftaki isme (değişkene) atar.:

  
>>> x = x + 1
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
NameError: name 'x' is not defined

Bir değişkeni güncellemeden önce, o değişkeni ilklemeniz gerekir, bu da oldukça basit bir atamayla yapılabilir:

  
>>> x = 0
>>> x = x + 1

Bir değişkeni üzerine 1 ekleyerek güncelleme işlemine artırma; değerinden 1 çıkarma işlemine çıkarma adı verilir.

6.3 `for` döngüsü

for döngüsünün listenin içindeki öğeler üzerinden döngü yaptığını hatırlayınız. Listenin içindeki eleman sırasıyla döngü değişkenine yeniden atanır ve döngünün içindeki gövde çalıştırılır.

  
for f in ["Jale", "Zerrin", "Burak", "Ahmet", "Zeki", "Tülay", "Perihan"]:
    davet_et= "Merhaba " + f + ". Lütfen Cumartesi Doğumgünü partime gelin."
    print(davet_et)

Liste içindeki bütün öğeleri teker teker taramaya gezinme (traversing) olarak isimlendireceğiz.

Öğeleri sayılardan oluşan bir listenin bütün öğelerini toplayan bir fonksyion yazalım. Bunu ilk önce el ile yapalım ve adım adım nasıl ilerleyeceğimiz fikrini kafamızda oluşturalım. Liste üzerinden bir yere kadar yaptığınız ara toplamı bir kağıt üzerinde, kafanızda veya hesap makinanızda tutmanıza ihtiyaç olacak. Programımızda değişkenlerin olmasının sebebi bir adımdan diğer bir adıma geçerken şeyleri hatırlamaktır. Bu yüzden “ara toplamı” hatırlayacak bazı değişkenlere ihtiyacımız olacak. Bu ara toplamın ilk başlangıçtaki değerini sıfır ile başlatmalıyız (ilklendirmeliyiz.) ve bu listenin öğeleri üzerinden gezinmeliyiz. Ara toplamaya sonraki bir sayıyı eklediğimizde, ara toplamayı güncelleştirmeliyiz.

  
def toplam(xs):
    """ xs listesi içindeki bütün öğelerin toplar ve bu sonucu geri döndürür."""
    ara_toplam = 0
    for x in xs:
        ara_toplam = ara_toplam + x
    return ara_toplam

# Fonksiyonun verdiği değerleri True ve False ile kontrol ediniz. 
print(toplam([1, 2, 3, 4]) == 10)
print(toplam([1.25, 2.5, 1.75]) == 5.5)
print(toplam([1, -2, 3]) == 2)
print(toplam([ ]) == 0)
print(toplam(range(11)) == 55)  # 11 listeye dahil değildir.

6.4 `while` döngüsü

Bilgisayarlar genellikle tekrarlayan görevleri otomatikleştirmek için kullanılmaktadır. Aynı veya benzer görevleri hatasız bir şekilde tekrarlama işlemi bilgisayarların iyi yaptığı, insanların zorlandığı bir şeydir.

Bir cümle kümesinin yinelemeli (tekrarlı) olarak yürütülmesi işlemine yineleme (iteration) adı verilir. Yineleme çok yaygın olduğu için, Python işlemi kolaylaştırmak için bir çok dil özelliği sağlamıştır. İnceleyeceğimiz bir diğer döngü while cümlesidir.

countdown isimli aşağıda tanımlanmış olan fonksiyon while cümlesinin nasıl kullanılacağını göstermektedir:

  
def countdown(n):
    while n > 0:
        print(n)
        n = n-1
    print("Yok ol!")

while cümlesini neredeyse İngilizce bir cümleymiş gibi okuyabilir ve yaptığı işi anlayabilirsiniz. Cümlenin anlamı n değişkeni sıfırdan (0) büyük olduğu sürece değerini ekranda görüntüle ve görüntülemeden sonra n’in değerini 1 azalt. Sıfır değerine ulaştığında (döngüden çık) ekranda Yok ol! kelimesini görüntüle

Daha biçimsel olarak, aşağıda while cümlesinin yürütme akışını (algoritmasını) inceleyebilirsiniz:

Koşulu değerlendir, False veya True üret
Eğer koşul yanlış ise, while cümlesinden çıkıp bir sonraki satırdan yürütmeye devam et.
Eğer koşul doğru ise, cümlenin gövdesindeki her cümleyi çalıştır ve 1. adıma geri dön.

Gövde başlığın altında eşit girintiye sahip olan tüm cümleleri içermektedir.

Bu şekildeki akışa döngü adı verilmektedir, çünkü üçüncü adımda işlem başa dönmektedir. Eğer koşul ilk seferinde yanlış ise, döngünün içerisindeki cümleler hiç bir zaman çalıştırılmazlar.

Döngünün gövdesi bir veya daha fazla değişkenin değerini değiştirmelidir ki, koşul yanlışlanabilsin ve döngünün bitmesi garanti edilsin. Eğer koşul yanlışlanamazsa döngü sonsuza kadar çalışabilir, bu şekildeki döngülere sonsuz döngü adı verilir. Bir bilgisayar bilimcisi için örneğin, şampuanların üzerindeki köpürtün, durulayın, tekrarlayın işlemi başlı başına bir sonsuz döngü eğlencesi yaratabilir.

countdown örneğinde,bu döngünün sonlandırıldığını ispatlayabiliriz, çünkü n değişkeninin sonlu olduğunu biliyoruz ve n değişkeninin her seferinde küçüldüğünü görebiliriz. Bu nedenlerden döngünün eninde sonunda biteceği kesindir. Ancak bazı durumlarda bunu görmek bu kadar kolay olmayabilir:

  
def sequence(n):
    while n != 1:
        print(n, end=" ")
        if n % 2 == 0:        # n çifttir
            n = n // 2
        else:                 # n tektir
            n = n * 3 + 1

Bu döngüdeki koşul n != 1‘dir, döngü koşulu yanlışlayan n 1 değerine sahip olana kadar devam edecektir.

Döngüdeki her seferde, program n‘nin değerini ekranda görüntüler ve değişkenin tek veya çift olup olmadığını sınar. Eğer çift ise değerini ikiye böler. Eğer tek ise değeri n * 3 + 1 ile değiştirilir. Örneğin, başlangıç argümanı olarak 3 verdiğimizi düşünelim, ortaya çıkan seri 3, 10, 5, 16, 8, 4, 2, 1.’dir.

n artabildiği ve azalabildiği için değerinin 1’e erişip erişmeyeceğine dair bir garanti yoktur. n‘nin bazı belirgin değerleri için yürütmenin biteceğini garantileyebiliriz. Örneğin, ikinin kuvvetlerini başlangıç değeri olarak kabul edersek n‘nin döngüde her seferinde ikiye bölünerek çift sayı olup 1’e ulaşacağını biliriz. Önceki örnek böyle bir seri ile (16 ile başlayan) bitmektedir.

Bazı özel değerleri bir kenara koyarsak, bu programın yürütmesinin tüm giriş değerleri için bitip bitmeyeceğini ispatlayabilir miyiz sorusu başlı başına ilginç bir sorudur. Şu ana kadar, bunu ispatlayan veya ispatlayamayan çıkmamıştır!

6.5 Programı izlemek

Etkili bilgisayar programları yazabilmek için, bir programcının bilgisayar programlarının yürütmesini izleme yeteneğini geliştirmesi gereklidir. İzleme bilgisayar olmayı ve bir örnek çalıştırarak yürütme akışını takip etmeyi gerektirir. Bu takipte her yürütülen bir satırdan sonra bütün değişkenlerin durumları ve programın ürettiği çıktıları kaydedilir.

Bu süreci anlamak için, sequence(3) çağrımını izlemeye çalışalım. İzlemenin başında n adında 3 ilk değerine sahip bir yerel değişkenimiz (başlangıç parametresi) vardır. 3, 1’e eşit olmadığı için while döngüsünün gövdesi çalıştırılır. 3 ekranda görüntülenir ve 3 % 2 == 0 deyimi değerlendirilir, sonuç False olduğundan, else dalı yürütülür ve 3 * 3 + 1 işlemi yapılır sonucu n değişkenine atanır.

Bütün bunları izleyebilmek için, bir kağıt parçasının üstüne yaratılan her değişken için başlık ve çıktı için bir başlık ekleriz. İzlememiz aşağıdaki gibi bir şey olacaktır:

   n              çıktı
  ---             ------
   3                 3
   10

10 != 1 ifadesinin değeri True olduğundan, döngü gövdesi tekrar yürütülecektir ve 10 ekranda görüntülenecektir. 10 % 2 == 0 doğru olduğundan, if dalı yürütülecek ve n 5 olacaktır. Bu izlemenin sonunda aşağıdakine sahip olmamız gerekir:

   n              çıktı
  ---             ------
               3
              10
               5
              16
               8
               4
               2
   1

İzleme can sıkıcı ve hataya eğilimli olabilir (bu yüzden bilgisayarları bu tür işler için kullanıyoruz), ancak bir programcının sahip olması gereken zorunlu yeteneklerden biridir. İzlemeyle kodumuzun nasıl çalıştığına dair bir çok şey öğrenebiliriz. n ikinin kuvveti olur olmaz, programın log2(n) yürütme sonunda döngü gövdesinden çıkacağını izleme sayesinde gözlemleyebiliriz. Ayrıca son 1’in çıktı olarak ekranda görüntülenmeyeceğini de bulabiliriz.

6.6 Basamakları sayma

Aşağıdaki fonksiyon bir sayının onluk basamaklarını pozitif tamsayı şeklinde onluk biçimde sayar:

  
def num_digits(n):
    count = 0
    while n:
        count = count + 1
        n = n // 10
    return count

Fonksiyonu num_digits(710) şeklinde çağırdığımızda 3 değerini ürettiğini görebilirsiniz. Bu fonksiyon çağrımının yürütmesini izleyerek çalıştığına dair kendinizi ikna edin.

Bu fonksiyon hesaplamanın sayaç adı verilen başka bir şablonunu göstermektedir. count değişkeni 0 ile ilklenmekte ve daha sonra döngü gövdesinde artırrılmaktadır. Döngü tamamlandıktan sonra, count sonucu – döngünün çalışma sayısı, ki bu toplam basamak sayısına eşittir – içerir.

Eğer sadece 0 veya 5 olan basamakları saymak isteseydik, arttırımdan önce bir koşul cümlesi koymamız işimize yarardı:

  
def num_zero_and_five_digits(n):
    count = 0
    while n:
        digit = n % 10
        if digit == 0 or digit == 5:
            count = count + 1
        n = n // 10
    return count

num_zero_and_five_digits(1055030250) ifadesinin 7 döndürdüğünü doğrulayın.

6.7 Kısaltılmış atama

Bir değişkeni arttırma Python’da sık karşılaşılan bir şeydir, bu nedenle bir kısaltması vardır:

  
>>> count = 0
>>> count += 1
>>> count
1
>>> count += 1
>>> count
2
>>>

count += 1 ifadesi count = count + 1 ifadesi yerine geçen bir kısaltmadır. Arttırma değeri 1 olmak zorunda da değildir:

  
>>> n = 2
>>> n += 5
>>> n
7
>>>

Diğer işleçler (-=, *=, /=, ve %=) için de kısaltmalar vardır:

  
>>> n = 2
>>> n *= 5
>>> n
10
>>> n -= 4
>>> n
6
>>> n /= 2
>>> n
3
>>> n %= 2
>>> n
1

6.8 Tablolar

Döngülerle ilgili olarak güzel şeylerden biri tablo biçiminde veri üretmede yararlı olmasıdır. Bilgisayarlar yok iken logaritma, sinüs, cosinüs ve diğer matematiksel fonksiyonların değerlerini insanlar el ile hesaplamak zorundaydı. Bunu kolaylaştırmak için matematik kitapları bu değerleri barındıran büyük değer tabloları içeriyordu. Bu tabloları hazırlamak yavaş ve sıkıcı bir işti, ve genellikle hatalar barındırıyordu.

Bilgisayarlar sahneye çıktıktan sonraki ilk tepkilerden biri Bu çok iyi birşey! Bilgisayarları tabloları üretmek için kullanabiliriz, böylece herhangi bir hata olmaz. idi. Bu tepkinin (çoğunlukla) doğru olduğu ama öngörüsüz olduğu ortaya çıktı. Bilgisayarların ve hesap makinelerinin her tarafa yayılmasından sonra, artık tablolara gerek kalmadı.

Tabi hemen hemen demek gerekiyor. Bazı işlemler için, bilgisayarlar yaklaşık yanıtı üretebilmek ve yaklaşık yanıtı iyileştirmek için hesaplamalar yapmak üzere tabloları kullanıyor. Bazı durumlarda, kaynak olarak kullanılan tablolarda bazı hatalar vardı, bunun en çok bilinen örneği Intel Pentium tarafından kayan noktalı sayılarda bölme işleminde kullanılan tabloydu.

Her ne kadar bir log tablosu eskisi kadar yararlı olmasa da, yinelemenin güzel bir örneğidir. Aşağıdaki program sol sütundaki değer dizisini ve sağ sütunda 2 sayısının bu değerden kuvvetini bir tablo şeklinde gösterir:

  
x = 1
while x < 13:
    print(x, '\t', 2**x)
    x += 1

‘\t’ ifadesi tab karakterisini temsil eder. ‘\t’ ifadesindeki ‘' karakteri kaçış serisi (escape sequence)nin başlangıcını belirtir. Kaçış serileri tab ve yeni satır gibi görünmez karakterleri göstermek için kullanılırlar. ‘\n’ serisi yeni satırı betimler.

Bir kaçış serisi bir karakter dizisinin herhangi bir yerinde bulunabilir; bu örnekte, tab kaçış serisi karakter dizisindeki tek şeydir. Bir karakter dizisinde ters bölü (‘') karakterini nasıl temsil edersiniz?

Karakter ve karakter dizileri ekranda görüntülendikçe, imleç (cursor) görünmeyen bir işaretçi bir sonraki karakterin nereye koyulacağını takip eder. print cümlesinden sonra, imleç normal olarak bir sonraki satırın başına gider.

Tab karakteri imleçi bir tab sonu ile karşılaşana kadar sağa kaydırır. Tablar metinleri sutünlar şeklinde hizalamak için yararlıdır, aşağıda önceki programın çıktısını inceleyebilirsiniz:

Sütunlar arasındaki tab karakterlerinden dolayı, ikinci sütunun konumu birinci sütundaki sayıların basamak sayısına bağlı değildir.

6.9 İki boyutlu tablolar

İki boyutlu bir tablo satır ve sütun kesişimindeki değeri okuduğunuz bir tablodur. Çarpım tablosu bu tür tablolar için iyi bir örnektir. 1’den 6’ya kadar çaprımları yazmak istediğinizi varsayalım.

Başlamak için iyi bir yol, tek bir kod satırında 2’nin çarpımlarını ekranda görüntüleyen bir döngü yazmaktır:

  
i = 1
while i <= 6:
    print (2*i,end="\t")
    i += 1
print()

İlk satır i ismindeki değişkeni ilkler, bu değişken sayaç veya döngü değişkeni şeklinde davranacaktır. Döngü işletildikçe i‘nin değeri 1’den 6’ya artar. i 7 olduğunda, döngü sonlandırılır. Döngünün her seferinde 2*i‘nin değeri boşluklardan sonra ekranda görüntülenir.

Yine, print cümlesindeki virgül yeni satıra başlamayı engeller. Döngü bittikten sonra, ikinci print cümlesi yeni bir satır başlatır.

Programın çıktısı:

2      4      6      8      10     12

Buraya kadar herşey güzel. Bir sonraki adım sarma (encapsulate) ve genelleştirme (generalization)dir.

6.10 Sarma (Encapsulation) ve genelleştirme

Sarma (encapsulation) bir kod parçasını fonksiyon içerisine koymadır. Böylece fonksiyonlar tarafından sağlanan tüm avantajlardan yararlanmış olacağız. Şimdiye kadar iki sarma örneği gördük: 4. bölümdeki print_parity ve 5. bölümdeki is_divisible fonksiyonları.

Genelleştirme özgü bir şeyi alıp, örneğin ikinin çarpım katlarını yazmak gibi, onu daha genel bir hale getirmektir, herhangi bir tamsayının tüm çarpım katlarını yazmak gibi.

Aşağıdaki fonksiyon bir önceki döngüyü sarıp genelleştirerek n tamsayısının çarpım katlarını ekranda görüntüler:

  
def print_multiples(n):
    i = 1
    while i <= 6:
        print(n*i, end='\t')
        i += 1
    print()

Sarmak için yapmamız gereken tek şey fonksiyon ismini ve parametre listesini tanımladığımız başlığı ilk satır olarak eklemektir. Genelleştirmek için, yapmamız gereken tek şey 2 değerini parametre olarak tanımladığımız n ile değiştirmektir.

Eğer bu fonksiyonu 2 argümanı ile çağırırsak, daha önceki çıktıyla aynı sonucu elde ederiz. Eğer argüman olarak 3 verirsek, çıktı aşağıdaki gibi olur:

3      6      9      12     15     18

Argüman olarak 4 verirsek, çıktımız:

4      8      12     16     20     24

Artık tahmin edeceğiniz gibi çarpım tablosunu nasıl ekranda görüntüleyeceğinizi – print_multiples fonksiyonunu farklı değerler için tekrar tekrar çağırarak – tahmin etmişsinizdir. Aslında başka bir döngü de kullanabiliriz:

  
i = 1
while i <= 6:
    print_multiples(i)
    i += 1

Bu yeni döngünün print_multiples içindeki döngüye ne kadar benzediğine dikkat edin. Yaptığımız tek şey print cümlesi yerine bir fonksiyon çağrımı – print_multiples – koymak oldu.

Bu programın çıktısı çarpım tablosudur:

    2      3      4      5      6
    4      6      8      10     12
    6      9      12     15     18
    8      12     16     20     24
    10     15     20     25     30
    12     18     24     30     36

6.11 Daha fazla sarma

Sarmayı tekrar göstermek için önceki bölümden bir kod alıp fonksiyon şekline getirelim:

  
def print_mult_table():
    i = 1
    while i <= 6:
        print_multiples(i)
        i += 1

Bu süreç yaygın karşılaşılan bir geliştirme planıdır. Kodu herhangi bir fonksiyon dışında yazarak veya yorumlayıcıya doğrudan yazarak geliştiririz, tam olarak çalışan koda ulaştığımızda bu kodu bir fonksiyon içerisine alıp, fonksiyon haline getiririz.

Bu geliştirme planı eğer programı hangi fonksiyonlara parçalayacağınızı bilmiyorsanız oldukça yararlıdır. Bu yaklaşım programı geliştirdikçe tasarlamanıza olanak sağlar.

6.12 Yerel değişkenler

Aynı değişkeni, i, hem print_multiples hem de print_mult_table fonksiyonlarının ikisinde nasıl kullanabildiğimizi merak ediyor olabilirsiniz. Bu fonksiyonlardan biri i‘nin değerini değiştirirse bu sorunlara yol açmaz mı?

Yanıt “hayır”dır, çünkü print_multiples ve print_mult_table fonksiyonlarındaki i değişkeni aynı değişken değildir.

Bir fonksiyon tanımlaması içerisinde yaratılan değişkenler yereldir; tanımlandığı ev fonksiyonu dışından bir yerden değişkene erişemezsiniz. Bunun anlamı aynı fonksiyon içerisinde tanımlı olmayan, aynı isme sahip birden fazla değişkene sahip olabilirsiniz.

Bu programdaki i isimli iki değişkeni gösteren yığıt diagramını aşağıda inceleyebilirsiniz. Farklı değerleri gösterebilirler ve birinin değişmesi diğerini etkilemez.

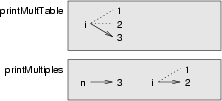
print_mult_table fonksiyonundaki i değişkeninin değeri 1’den 6’ya artar. Şekilde 3’tür. Bir sonraki döngüde 4 olacaktır. Döngüdeki her seferde, print_mult_table fonksiyonu print_multiples fonksiyonunu i değişkeninin o anki değerini argüman olarak kullanarak çağırmaktadır. Bu değer n parametresine atanmaktadır.

print_multiples içerisinde, i değişkeninin değeri 1’den 6’ya artmaktadır. Şekilde 2’dir. Bu değişkeni değiştirmenin print_mult_table fonksiyonu içerisindeki i üzerinde bir etkisi yoktur.

Aynı isimde farklı yerel değişkenlere sahip olmak, sık karşılaşılan ve tamamen geçerlidir. Aslında i ve j gibi isimler döngülerde değişken ismi olarak sıklıkla kullanılmaktadır. Eğer başka bir fonksiyon içerisinde kullandığınız için kullanmamazlık ederseniz, programın okunmasını zorlaştırırsınız.

6.13 Daha fazla genelleştirme

Genelleştirmeye başka bir örnek olarak sadece 6x6 değil herhangi bir boyutta çarpım tablosu yazdırma isteğimizi verebiliriz, print_mult_table fonksiyonuna bir parametre ekleyerek bunu gerçekleştirebiliriz:

  
def print_mult_table(high):
    i = 1
    while i <= high:
        print_multiples(i)
        i += 1

6 değerini high parametresi ile değiştirdik. Eğer print_mult_table fonksiyonunu 7 argümanı ile çağırırsak, aşağıdaki sonucu üretecektir:

    2      3      4      5      6
    4      6      8      10     12
    6      9      12     15     18
    8      12     16     20     24
    10     15     20     25     30
    12     18     24     30     36
    14     21     28     35     42

Tablonun kare olmasını (satır ve sütun sayısının eşit olması) isteyebileceğimiz dışında bu yeterli bir çözüm. Tabloyu kare haline getirmek için print_multiples fonksiyonuna sütun sayısını belirleyecek olan başka bir parametre ekleriz.

Can sıkmak için, bu parametreyi de high olarak adlandıralım, böylece farklı fonksiyonların aynı isme sahip (yerel değişkenler gibi) parametrelere sahip olabileceğini göstermiş oluruz. Programın son hali şekildedir:

  
def print_multiples(n, high):
    i = 1
    while i <= high:
        print(n*i, end='\t')
        i += 1
    print()
   
def print_mult_table(high):
    i = 1
    while i <= high:
        print_multiples(i, high)
        i += 1

Yeni bir parametre eklediğimizde fonksiyonun ilk satırını (fonksiyon başlığı) değiştirdiğimiz farketmişsinizdir. Buna ek olarak fonksiyonun çağrıldığı yerleri (örneğin print_mult_table içinde çağrılan yer) de değiştirmemiz gerekmektedir.

Beklediğimiz gibi, bu program tabloyu 7x7 boyutlarında kare şeklinde üretir:

    2      3      4      5      6      7
    4      6      8      10     12     14
    6      9      12     15     18     21
    8      12     16     20     24     28
    10     15     20     25     30     35
    12     18     24     30     36     42
    14     21     28     35     42     49

Bir fonksiyonu uygun şekilde genelleştirdiğinizde, planlamadığınız yeteneklere sahip bir program elde edersiniz. Örneğin ab = ba olması dolayısıyla tablodaki her bir girdinin iki kere görüntülendiğini farketmişsinizdir. Mürekkep harcamasını azaltmak için tablonun sadece yarısını görüntülemek isteyebilirsiniz. Bunu yapmak için print_mult_table fonksiyonunda bir satır değiştirmeniz gerekir. Aşağıdaki satırı

  
print_multiples(i, high)

aşağıdaki şekilde

  
print_multiples(i, i)

değiştirdiğinizde şu sonucu üretebilirsiniz:

1
    4
    6      9
    8      12     16
    10     15     20     25
    12     18     24     30     36
    14     21     28     35     42     49

6.14 Fonksiyonlar

Şimdiye kadar bir kaç kere fonksiyonlar için iyi olan şeylerden bahsettik. Bu noktada, iyi olan bu şeylerden bir kısmını toplu bir şekilde vermemiz aydınlatıcı olacaktır:

Bir cümle dizisine bir isim vermeniz programınızın okunabilirliğini arttıracak, hata ayıklamayı kolaylaştıracaktır.
Büyük bir programı fonksiyonlara parçalamanız, programda parçaları birbirinden ayırmanızı sağlayacaktır. Böylece izole bir şekilde hataları ayıklayabilecek, bu farklı parçaların bir bütün olarak davranmasını sağlayabileceksiniz.
Fonksiyonlar yinelemenin kullanımını kolaylaştırır.
İyi tasarlanmış fonksiyonlar, yazılıp iyi bir şekilde hatalardan arındırıldıktan sonra tekrar kullanılabildiği için, bir çok program için yararlıdır.

6.15 Newton yöntemi

Döngüler, bir yaklaşık değer ile başlayıp yineli olarak bu yaklaşık değerin iyileştirildiği nümerik hesaplamalarda sıklıkla kullanılmaktadır.

Örnek olarak, kare kök hesaplamada kullanılan Newton yöntemini verebiliriz. Farzedelim ki, n değişkeninin kare kökünü bulmak istiyoruz. Herhangi bir yaklaşık değer ile başlarsak, aşağıdaki formülü kullanarak daha iyi bir yaklaşık değer (başladığımız yaklaşık değeri iyileştirerek) hesaplayabiliriz:

  
better =  (approx + n/approx)/2

Bu formülü, yeni elde ettiğimiz yaklaşık değer önceki değerden farklı olduğu sürece (better!=approx) yineleyerek kullanan bir kare kök hesaplama fonksiyonu yazabiliriz:

  
def sqrt(n):
    approx = n/2.0
    better = (approx + n/approx)/2.0
    while better != approx:
        approx = better
        better = (approx + n/approx)/2.0
    return approx

Bu fonksiyonu 25 değeri için çağırın ve fonksiyonun 5.0 sonucu üretip üretmediğini sınayarak doğru çalışıp çalışmadığını kontrol edin.

6.16 Algoritmalar

Newton yöntemi bir algoritma örneğidir: belli bir kategorideki (bu durumda kare kökleri hesaplama kategorisi) problemleri çözmeye yönelik mekanik bir süreçtir.

Bir algoritmayı tanımlamak kolay değildir. İlk olarak algoritma olmayan bir şey ile başlamak yardımcı olacaktır. Tek basamaklı sayıları çarpmayı öğrendiğinizde, çarpım tablosunu ezberlemişsinizdir. Bunun sonucunda, 100 belli çözümü ezberlediniz. Bu tür bilgi algoritmik değildir.

Eğer tembel biriyseniz, bir kaç ipucu kullanarak öğrenip hile yapmışsınızdır. Örneğin n ve 9’un çarpımını bulmak için n-1 ilk basamak, 10-n ikinci basamak olacak şekilde yazarak sonucu üretmişsinizdir (7x9 = 63’ü düşünün). Bu “hile” herhangi tek basamaklı bir sayı ile 9 u çarpmak için genel çözümdür. Bu bir algoritmadır!

Benzer olarak, eldeli toplama, borçlu çıkarma ve uzun bölme işlemleri için öğrendiğiniz tekniklerin hepsi algoritmalardır. Algoritmaların temel özelliği uygulanabilmeleri için özel bir zeka gerektirmemeleridir. Basit kurallara göre her bir adımın birbirini izlediği tamamen mekanik süreçlerdir.

Bizim düşüncemize göre, insanların okulda herhangi bir zeka gerektirmeyen algoritmaları yürütmeyi öğrenmek için çok fazla zaman harcamaları utandırıcı bir durumdur.

Diğer taraftan, algoritma tasarımı süreci ilginç, zihni zorlayıcı ve programlamanın temel parçası olan bir süreçtir.

İnsanların zorlanmadan veya bilinç dışı olarak doğallıkla yaptığı bazı şeyleri algoritmik olarak ifade etmek zordur. Doğal dili anlamak bunun güzel bir örneğidir. Hepimiz bunu yapıyoruz ama nasıl yaptığımızı şimdiye kadar kimse tam olarak anlatamamıştır. En azından bu işlemi herhangi bir algoritmik biçimde yapmıyoruz.

6.17 Sözlük

birden fazla atama:: Programın yürütülmesi esnasına bir değişkene birden fazla atama yapılması
(değişken) ilkleme:: Bir değişkeni ilklemek (initialize), değişkene bir başlangıç değeri verilmesidir, genellikle birden fazla atama durumlarında yapılır. Python’da değişkenler atama yapılmadığı sürece varolmadıkları için, yaratıldıkları zaman ilklenirler. Diğer programlama dillerinde durum bu şekilde değildir, ve değişkenler ilklenmeden de yaratılabilir, ilk değer olarak ya varsayılan değeri, ya da çöp, anlamsız değeri barındırırlar.
arttırma: İsim ve sıfat olarak, arttırma bir değere 1 ekleme anlamına gelir.
azaltma: 1 çıkarma.
yineleme:: Programlama cümlesi kümesinin tekrar tekrar çalıştırılması.
döngü:: Bitiş kriteri karşılanana kadar tekrar tekrar çalıştırılan bir cümle veya cümle grubu.
sonsuz döngü:: Bitiş kriterinin hiç bir zaman karşılanamadığı döngü.
izleme:: Bir programın yürütme akışını elle takip etme, değişken durumlarındaki değişimleri ve üretilen çıktıları kaydetme işlemidir. sayaç Bir şeyi saymak için kullanılan değişken, genellikle sıfır olarak ilklenip bir döngü gövdesinde arttırılır.
gövde:: Bir döngü içerisindeki cümleler.
döngü değişkeni:: Bir döngünün bitiş kriterinin bir kısmı olarak kullanılan değişken.
tab:: İmlecin bulunulan satırda bir sonraki tab durma noktasına hareket etmesini sağlayan özel karakter.
yeni satır:: İmlecin bir sonraki satırın başına konumlanmasını sağlayan özel karakter.
imleç:: Bir sonraki karakterin nereye yazılacağını tutan görünmez işaretçi.
kaçış dizisi:: Bir kaçış karakteri, \, ve onu takip eden yazılabilir bir veya daha fazla karakterden oluşan yazılmayan bir karakteri belirtmek için kullanılan karakter dizisi.
sarma (encapsulation):: Büyük karmaşık bir programı bileşenlere (fonksiyonlar gibi) bölme (parçalama, ayırma) ve her bir bileşeni diğerlerinden yalıtma (örneğin yerel değişkenleri kullanarak) işlemidir.
genelleştirme:: Gereksiz yere özel olan bir ifadeyi (sabit bir değer gibi), uygun bir şekilde genel olan bir ifadeyle (bir değişken veya parametre gibi) değiştirme işlemidir. Genelleştirme kodu çok yönlüleştirir, tekrar kullanılabilirliğini arttırır, hatta yazılması işlemini kolaylaştırabilir.
geliştirme planı:: Bir programı geliştirme sürecidir. Bu bölümde basit, belli şeyleri yapıp bunları sarıp, genelleştirilmesine dayanan bir kod geliştirme süreci anlatılmıştır.
algoritma:: Belli bir kategorideki problemleri adım adım çözme sürecidir.

6.18 Alıştırmalar

Aşağıdaki çıktıyı üreten tek bir karakter dizisi yazın

   bu
   çıktıyı
   üretmeli.

6.14 bölümünde tanımlanan sqrt fonksiyonuna better değişkeni her hesaplandığında ekranda görüntüleyen bir print cümlesi ekleyin. Fonksiyonun değiştirdiğiniz halini 25 argümanı ile çağırıp, sonuçları kaydedin.
print_mult_table fonksiyonunun son sürümünün yürütmesini izleyip, nasıl çalıştığını anlamaya çalışın.
Adı print_triangular_numbers(n) olan ve ilk üçgen sayıları ekranda görüntüleyen bir fonksiyon yazın. print_triangular_numbers(5) çağrımı aşağıdaki çıktıyı üretmelidir:

(ipucu: bir web araması yaparak üçgensel sayının ne olduğunu bulabilirsiniz.)

Adı ch06.py olan bir dosya yaratıp içerisine aşağıdakileri ekleyin:

  
if __name__ == '__main__':
    import doctest
    doctest.testmod()

is_prime isminde, tek bir tamsayı argüman alan ve eğer argüman asal sayı ise True döndüren, değilse False döndüren bir fonksiyon yazın. Fonksiyonunu geliştirirken doctestlerini de ekleyin.

num_digits(0) ne döndürecektir?

Bu durum için 1 döndürecek şekilde fonksiyonu düzeltin. Neden num_digits(-24) çağrımı sonsuz bir döngü oluşturmaktadır (ipucu: -1/10 değeri -1 olarak değerlendirilmektedir)? num_digits fonksiyonunu herhangi bir tamsayı değerler doğru çalışacak şekilde düzeltin.

Daha önceki alıştırmada hazırladığınız ch06.py dosyasına aşağıdakileri ekleyin:

  
def num_digits(n):
    """
 >>> num_digits(12345)
 5
 >>> num_digits(0)
 1
 >>> num_digits(-12345)
 5
 """

Fonksiyon gövdenizi num_digits fonksiyonuna koyup tüm dostestleri geçtiğini doğrulayın.

Aşağıdakileri ch06.py içerisine koyun:

  
def num_even_digits(n):
    """
 >>> num_even_digits(123456)
 3
 >>> num_even_digits(2468)
 4
 >>> num_even_digits(1357)
 0
 >>> num_even_digits(2)
 1
 >>> num_even_digits(20)
 2
 """

num_even_digits fonksiyonuna beklendiği gibi çalışacak bir gövde yazın.

Aşağıdakiler ch06.py dosyasına ekleyin:

  
def print_digits(n):
    """
 >>> print_digits(13789)
 9 8 7 3 1
 >>> print_digits(39874613)
 3 1 6 4 7 8 9 3
 >>> print_digits(213141)
 1 4 1 3 1 2
 """

print_digits fonksiyona tüm verilen doctestleri geçebileceği bir gövde yazın.

Adı sum_of_squares_of_digits olan bir fonksiyon yazın. Bu fonksiyon argüman olarak verilen tamsayının tüm basamaklarının karelerini toplasın. Örneğin, sum_of_squares_of_digits(987) 194 döndürmelidir, çünkü 9**2 + 8**2 + 7**2 == 81 + 64 + 49 == 194‘tür.

  
def sum_of_squares_of_digits(n):
    """
 >>> sum_of_squares_of_digits(1)
 1
 >>> sum_of_squares_of_digits(9)
 81
 >>> sum_of_squares_of_digits(11)
 2
 >>> sum_of_squares_of_digits(121)
 6
 >>> sum_of_squares_of_digits(987)
 194
 """

Çözümünüzü yukarıdaki doctestler bağlamında sınayın.