Algoritma Analizi Nedir? Zaman Karmaşıklığı ve Big O Notasyonu

Algoritma Analizi Nedir?

Algoritma analizi, algoritmanın yürütülmesi için gerekli kaynak miktarının belirlenmesidir. Belirli bir problemi çözen herhangi bir algoritmanın ihtiyaç duyduğu kaynaklar için teorik tahminler sağlar. Başka bir ifadeyle, algoritmanın performansı ve kaynak kullanımı konusunda yapılan teorik çalışmaların tümüne algoritma analizi denir.

Buradaki çalışmalar, herhangi bir programlama dilinden bağımsız bir şekilde yürütülür ki gerçek anlamda sadece algoritmanın kendisini analiz edip bilimsel bir yaklaşım benimseyebilelim.

Aslında belli bir makinede çalıştırılabilir algoritmaların performansı için dikkat etmemiz gereken kriterler arasında ‘programlama dili seçiminin’ yanı sıra birçok teknoloji detayı vardır ki bunlar; derleyici seçimi, kodu hangi hızda çalıştırdığımız, belleğin ne kadar hızlı olduğu ve hatta önbelleğe alma işleminin miktarı olarak sıralanabilir.

Bu kriterler, spesifik bir işlemin verimliliği açısından algoritmanın çalışma süresini tahmin etmek için önemli olsa da algoritmanın kendisini analiz etmek için gerekli temel kıstaslardan değildir. Bu kıstasları veya kriterleri ileride göreceğiz ancak öncesinde, algoritma analizine neden ihtiyaç duyduğumuzu açıklayalım.

Algoritma Analizine Neden İhtiyaç Duyarız?

Gerçekten Gerekli mi?

Nasıl ki günlük hayatta ‘vakit nakittir’ deyimi birçok alanda karşılığını buluyorsa, programlamada da durum böyledir. Büyük bir miktarda veriyi işlerken bunu olabildiğince hızlı yapmak isteriz. Buradaki hızlı ve yavaş kavramları, girdi boyutu ile doğrudan ilişkilidir. Örneğin 10 tane veriyi 1000 tane veriye göre çok daha hızlı sıralayabiliriz.

Ama bu, algoritmanın daha hızlı olması için daha az girdiye sahip olması gerektiği gibi saçma bir sonuç çıkarmamalı. Yani girdi miktarını örneklendirerek kıyas yaparız ve bir tahminde bulunuruz. Çünkü işlenmesi gereken veri miktarı çoğu zaman kesin olarak bildiğimiz bir şey değildir. İşte bu yüzden, emin olamadığımız sayıda veri girişi içeren bir algoritmayı tasarlamak veya tercih etmek için analize ihtiyaç duyarız.

Ek olarak, programlamada problem çözme kabiliyeti, yapılan işin kalitesi açısından çok önemlidir. Bir problemin çözümü için gelişigüzel mantıklar kurmak ya da aynı şekilde rastgele algoritma tercihi yapmak programın kalitesinden ödün vermek demektir. Evet, belirli bir problemi farklı algoritmalar ile pek tabii çözebiliriz ancak o probleme özel olan en uygun çözümü getirecek algoritmayı belirlemek, belki de problemi çözmekten çok daha önemlidir ve gereklidir.

Çünkü günün sonunda algoritma bir şekilde oluşur ve sorun çözülür ama her bakımdan maksimum performansı elde eden tek bir algoritma vardır.

İşte o algoritmayı bulmak, diğer algoritmalarla arasındaki farkları ve avantajları belirlemek veya kısaca kıyas yapmak için algoritma analizine ihtiyaç duyarız. Bazen de karşılaştırma yapmaktan ziyade sadece bir algoritmanın performansını ölçmek için analize ihtiyaç duyarız. Peki, algoritma analizinde kıyas yapmak veya performans ölçmek için gerekli kıstaslar nelerdir?

Algoritmanın Performans Kriterleri Nelerdir?

Algoritma verimliliğinde ya da performansında iki kriter vardır. Bunlar zaman(time) ve alan(space) kavramlarıdır. Aslında amacımız bu kavramlar ışığında aşağıdaki sorulara cevap aramak olacaktır.

• Zaman (time)
  • Algoritma ne kadar hızlı performans gösteriyor?
  • Algoritmanın çalışma zamanını ne etkiler?
  • Algoritma için gerekli olan zaman nasıl tahmin edilebilir?
  • Algoritma için gerekli olan zaman nasıl azaltılabilir?
• Alan (space)
  • Hangi veri yapısı ne kadar yer kaplar?
  • Ne tür veri yapıları kullanılabilir?
  • Veri yapısı seçimi çalışma zamanını nasıl etkiler?

Bu noktada yürütme zamanı, zaman karmaşıklığı, alan maliyeti ve alan karmaşıklığı gibi kavramlar karşımıza çıkıyor. Algoritma analizinde daha çok yürütme zamanı ve zaman karmaşıklığı üzerinde yoğunlaşacağız ancak diğer kavramlara da bakmakta fayda var.

Alan Maliyeti Nedir? (Space Coast)

Algoritmanın işlevini yerine getirmesi için gereken bellek miktarına veya o bellek alanını veren bağıntıya alan maliyeti denir. Alan maliyeti program kodu, yığın ve veri için gerekli tüm alanları kapsar. S(n) şeklinde gösterilir.

Ek olarak, 4 bytelık tamsayı olan n elemanlı bir küme için alan maliyeti bağıntısı S(n)=4n şeklinde ifade edilmektedir.

Alan Karmaşıklığı Nedir? (Space Complexity)

Alan karmaşıklığı, bir algoritma veya işlemin girdi boyutuna göre çalıştırması gereken toplam bellek miktarını ölçer. Yani alan maliyetini ölçmek demektir diyebiliriz.

Baştaki analiz tanımında da söylediğimiz gibi, alan karmaşıklığı programlama dili, derleyici ve hatta algoritmayı çalıştıran makine gibi çeşitli faktörlere bağlıdır. Bu yüzden algoritmanın kendisini analiz ederken bu faktörleri dikkate almıyoruz. Ek olarak, ne yazık ki, algoritma verimliliğinde alan ve zaman iki ayrı kutup gibidir. Hızın artırılması çoğu zaman bellek tüketiminin artmasına neden olur, aynı şekilde bunun tersi de geçerli olabilir.

Alan karmaşıklığı analizi sonucunda;

“-bir tarafta, son derece hızlı olan ancak çok fazla bellek gerektiren merge sort algoritması, diğer tarafta, yavaş bir algoritma olan ama az bellek tüketen bubble sort algoritması, arasında ise diğer ikisine nazaran daha dengeli olan in-place heap algoritması bulunmaktadır.”

gibi çıkarımlar yapabiliriz.Bu ikilemlere sahip algoritmaların tercihinde, üzerinde çalışılan programın isterleri de göz önünde bulundurulabilir.

Yürütme Zamanı veya Çalışma Zamanı Nedir?

(Running Time)

Yürütme zamanı, ‘n’ boyutlu bir problemin algoritmasını çalıştırmak için gerekli olan zamana denir. Başka bir ifadeyle karşılaştırma, döngü çevirimi, aritmetik işlemler gibi algoritmanın işlevini yerine getirmesi için temel kabul edilen işlemlerin kaç kere yürütüldüğünü veren bir bağıntıdır.

Örneğin n elemanlı bir küme için yürütme zamanı T(n) şeklinde gösterilir. Ayrıca algoritmadaki eleman sayısı fazlalaştığında yürütme zamanı, birazdan göreceğimiz zaman karmaşıklığı olarak da adlandırılır. Aslında yapılan iş bakımından yürütme zamanı ile zaman karmaşıklığı benzer olsa da zaman karmaşıklığını yürütme zamanından ayıran çok önemli ayrıntılar var, ileride göreceğiz.

Çalışma süresi hesabında dikkat edeceğimiz temel hesap birimleri göz atalım.

• Programlama dilindeki deyimler
• Döngü sayıları
• Toplam işlem sayısı
• Dosyaya erişim sayısı
• Atama sayısı

Örnek olması açısından, aşağıdaki Python fonksiyonunun yürütme zamanını bulalım.

def topla(dizi, N):
	topla, i = 0, 0
	while(i < N):
		topla += dizi[i]
		i += 1
	return topla

Görüldüğü gibi ‘topla’ isimli fonksiyonda ilk olarak, 2. satırdaki topla ve i değişkenlerine atama işlemi yapıyoruz ve toplamda 2 işlem yapmış oluyoruz. Daha sonra 3. satırda while döngüsü için dizi boyutu olarak gönderilen N değişkeninin bir fazlası kadar kontrol işlemi yapılıyor ki buradaki toplam işlem sayısı da N + 1 şeklinde oluyor.

Şu ana kadarki genel toplam 2 + N + 1 = 3 + N oldu. Devam edecek olursak 4. ve 5. Satırda da N tekrardan toplam 2N şeklinde bir tekrar olur ve genel toplam 3N + 3 olur ve buna T(N) = 3N + 3 şeklinde çalışma zamanı deriz.

Daha iyi kavramak için faktöriyel hesabı yapan C fonksiyonunun çalışma zamanını bulalım.

int faktoriyel(int n){
	if (n <= 1)
		return 1;
	else
		return (n * faktoriyel(n - 1));

}

Burada da gördüğünüz gibi 2. satırda n tekrar, 3. satırda 1 tekrar, 5. satırda ise recursive şekilde fonksiyon çağırımı yapan ve ilk gönderilen sayının 1 eksiği kadar tekrarı olan bir işlem bulunmaktadır. Yani toplamda 2n kadar bir tekrar olacak ve T(n) = 2n şeklinde ifade edilecek.

Şimdi ise, argüman olarak aldığı dizideki en küçük elemanı bulan bir algoritmaya bakalım.

int bulEnkucuk(int A[], int n){
	int enkucuk;
	int k;
	enkucuk = A[0];
	for (k = 0; k < n; k++)
		if (A[k] < enkucuk)
			enkucuk = A[k];
	return enkucuk;
}

Burada, ilk olarak 4. satırda enkucuk isimli değişkene, tekrarı 1 olacak şekilde bir atama işlemi yapılıyor. Daha sonra for döngüsünde k değerine 0 ataması 1 kez, k değerinin n(dizideki eleman sayısı) değerinden küçük olup olmadığı kontrolü n+1 kez ve k değerini artırma işlemi n kez yapılıyor. Buraya kadar genel toplam 2n+3 oluyor.

Devam edecek olursak, koşul ifadesinde dizinin boyutu kadar tekrar eden bir kontrol işlemi var ancak if bloğunun içinde kalan enkucuk adlı değişkene yapılan atama işlemi n-1 kez tekrar etmekte. Çünkü A[k] değeri ile enkucuk isimli değişken, birbirine bir kez denk olacak ve en az bir kez if bloğunun içine girilmeyecek.

Tabii, buradaki gönderilen dizinin, küçükten büyüğe sıralanmış şekilde gelmesini hesaba katmadan, en kötü ihtimale göre tekrar işlemini değerlendiriyoruz. Aksi takdirde, if bloğuna hiç girilmeye de bilir.

 Bunu zaman karmaşıklığında, tekrar sayıları sonsuza giderken çok daha iyi anlayacağız çünkü tekrar sayılarının sonsuza gitmesini ele alırken, değil en iyi ihtimali göz önünde bulundurmak, 1 kez tekrar eden sabitler bile bir anlam ifade etmeyecek. Çok fazla uzatmadan, son bir örnekle çalışma zamanı hesabını bitirelim.

void toplamMatris(int A[2][2], int B[2][2])

{
	int C[2][2];
	int i, j;
	for (i = 0; i < 2; i++)
		for (j = 0; j < 2; j++)
			C[i][j] = A[i][j] + B[i][j];

}

Burada, 2 satırdan ve 2 sütundan oluşan iki matrisin toplamını geri döndüren bir fonksiyon bulunmakta. Matris boyutundan bağımsız bir şekilde önceki örneklerde olduğu gibi uzunluğu n alacak olursak, 4. satırda sırasıyla 1, n+1 ve n kez tekrar eden işlemler var. Bu şekilde toplam tekrar sayısı 2n+2 olur. 

5 inci satırda bulunan for döngüsünde ise uzunluğu m alacak olursak, dıştaki for döngüsüne bağlı bir tekrar sayısı çıkacak. Yani 2m+2 olan tekrar sayısı, n kadar tekrar edeceğinden 2m+2 ifadesini n ile çarparak tekrar sayısını bulacağız. Sonuç olarak 5. satırdaki toplam tekrar sayısı n ve m`ye bağlı olarak 2nm+2n çıkmaktadır. 

Buraya kadarki genel toplam ise 2nm+4n+2 oldu. Son olarak 6. Satırda iki döngünün tekrarının çarpımı kadar tekrar sayısı oluşacak. Böylelikle son toplam 3nm+4n+2 olmaktadır ve T(n) = 3nm+4n+2 şeklinde gösterilmektedir.

Zaman Karmaşıklığı Nedir? (Time Complexity)

Zaman karmaşıklığı, bir algoritmadaki yürütme zamanının derecesinin asimptotik notasyonlarla gösterilmesine denir. Başka bir ifadeyle, algoritmanın asimptotik notasyona göre karmaşıklık mertebesidir.

Burada amaç, yürütme zamanında da dediğimiz gibi algoritmadaki eleman sayısı çok fazla olduğunda ya da veri seti sonsuza gittiğinde, giriş boyutu ve zaman arasındaki karmaşıklığı azaltmaktır. Yani detaylardan kurtularak çalışma süresi analizini basitleştirmektir. 

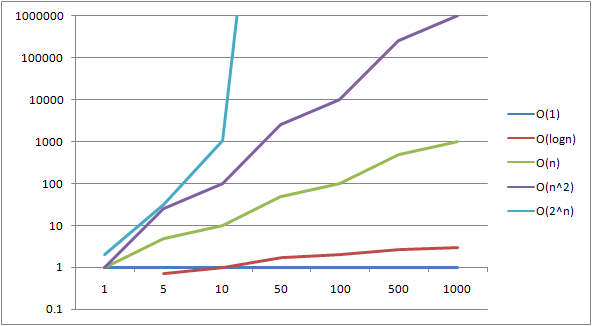
Fonksiyonlara Göre Zaman Karmaşıklığı

Bunun için asimptotik gösterimde, fonksiyon içerisindeki sabitler ve katsayılar gibi sonsuza giderken büyümeye pek etkisi olmayan önemsiz kısımlar atılır. Böylelikle geriye, verinin büyümesine bağlı olarak fonksiyonun büyümesinde en büyük etkiye sahip olan parametre kalır ve gerçek fonksiyona göre yaklaşık bir değer bulunabilir.

Burada zaman karmaşıklığı için karşımıza üç temel asimptotik notasyon çıkmakta, bunlar;

• Big-O notasyonu / Büyük O Notasyonu / Big O gösterimi (ya da Big-Oh)
• Omega notasyonu / Omega gösterimi / Big-Ω
• Teta notasyonu / Teta gösterimi / Big-θ

Biz daha çok Big-O notasyonu ile ilgileneceğiz. Bunun nedenini anlamak için best case (en iyi durum), average case (ortalama durum), worst case (en kötü durum) gibi kavramları bilmemiz gerekiyor.

Best Case (En iyi durum): Algoritmada yürütme zamanı, maliyet ve karmaşıklık hesaplanırken en iyi sonucun elde edildiği duruma denir. Yani algoritmanın en az adımda ve en kısa sürede çalıştığı giriş durumudur. Çalışma zamanında bir alt sınırdır. Daha iyisi yoktur. Grafik gösterimlerinde lower bound (alt sınır) olarak da karşımıza çıkabilir.

Worst Case (En kötü durum): Adında da anlaşılacağı gibi best case durumunun tam tersidir. Olabilecek en olumsuz koşulları içinde barındıran durumdur.

 Örnek olarak, dizi elemanlarını küçükten büyüğe sıralama işlemini yapan bir algoritmaya girdi olarak tam tersi şekilde tam olarak büyükten küçüğe doğru sıralanmış bir dizi göndermek en kötü durumdur. Ya da bir arama algoritmasındaki veri setinde kontrol edilen ilk değerin, aranan değer olması best case iken aranan değerin veri setinin son konumunda bulunması veya hiç bulunmaması worst case`e örnektir.

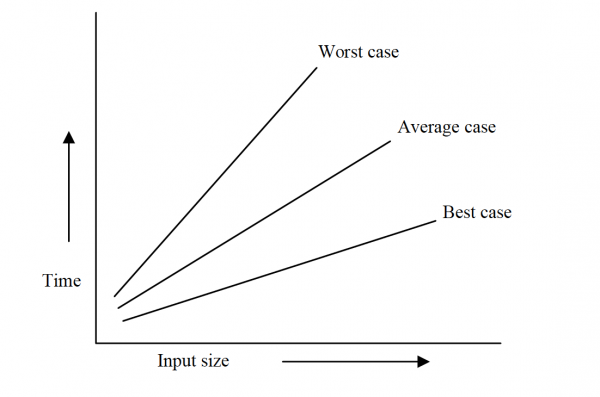
Algoritma Analizinde Worst Case - Best Case- Average Case

Yine, en iyi durumdaki gibi, grafik gösterimlerinde upper bound olarak da karşımıza çıkabilir. Bu, bir algoritma upper bound`dan daha yavaş çalıştırılamaz demektir.

Average Case (Ortalama Durum): Tahmin ettiğiniz gibi sonuçları en kötü olan durum ile en iyi durum arasında çıkan durumdur. Ortalama bir değerdir.

Bu üç durumu incelediğimize göre, karmaşıklık analizinde neden daha çok Big-O notasyonuyla ilgilendiğimize bakalım. Daha önce de söylediğimiz gibi, karmaşıklık analizinde verileri sonsuza giderken değerlendiririz.

Aşağıdaki TA ve TB fonksiyonların çalışma zamanının, veri boyutuna göre nasıl değiştiğini gözlemleyelim.

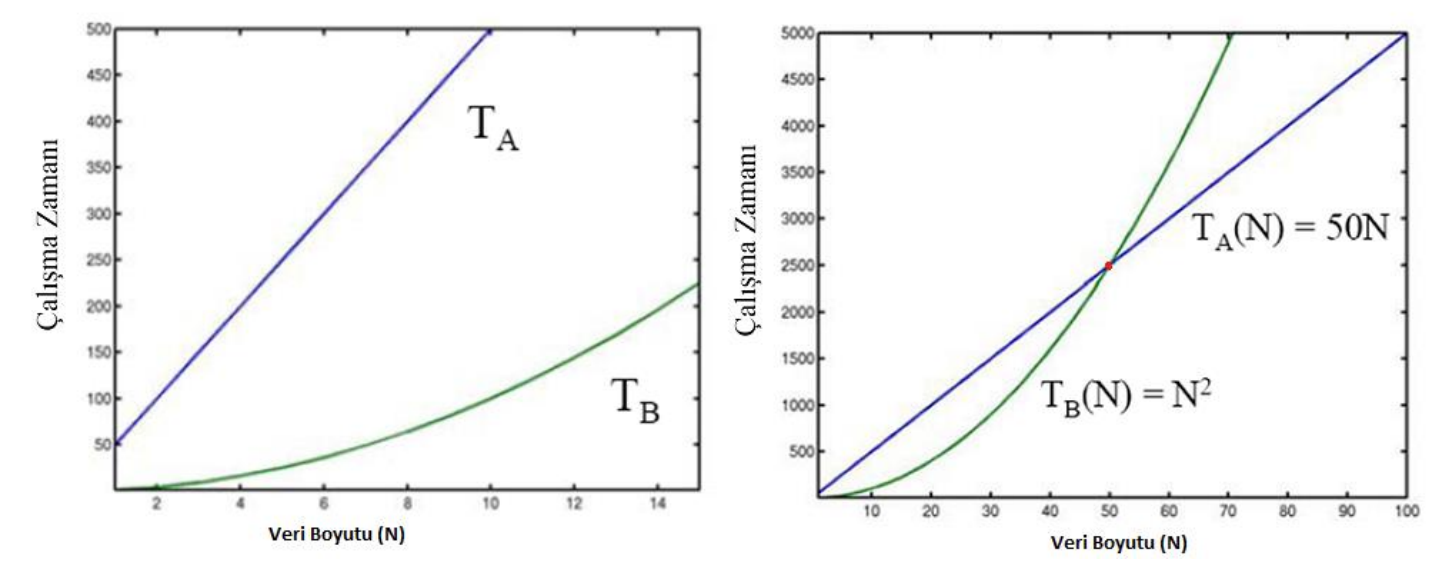
Algoritma Analizinde Zaman Karmaşıklığı - Büyüme Oranı

İlk grafikteki veri girişi, ikinci grafiğe göre daha az iken TB fonksiyonunun verimliliği daha iyi gibi gözüküyor ancak ikinci grafikte, veri boyutu 50 olduktan hemen sonra verimlilik, zaman kıstasına göre düşüyor.Bu yüzden veri girişinin sonlu olmadığı durumlara, en kötü senaryoya, algoritmanın üst sınırına(upper bound) bakmamız gerekiyor.

İşte Big O notasyonu bize, algoritmanın üst sınırını, upper bound değerini yani worst case`ini verir. Bu şekilde algoritmanın büyüme oranındaki (growth rate) en kötü senaryosunu görebiliriz.

Şimdi, Big O notasyonuna geçmeden önce diğer notasyonların da ne olduğuna kısaca bir bakalım.

Omega Notasyonu Nedir? Big-Ω Notasyonu Nedir?

Omega notasyonu (Omega Notation), asimptotik bir alt sınırı(lower bound) ifade eder. Dolayısıyla, bir algoritmanın karmaşıklığını Büyük-O gösterimine zıt olarak verir. Bu notasyon sayesinde, zaman açısından best case`e ulaşmış oluruz.

Aynı zamanda, veri girişi tarafında, “kaplanılan alan miktarı, şuan ki değerden daha yavaş bir şekilde büyümeyecek ama daha hızlı büyüyebilir” gibi çıkarımlar da yapabiliriz.

Teta Notasyonu Nedir? Big-θ Notasyonu Nedir?

Teta gösterimi, lower bound ile upper bound sınırları içinde olan bir durumu temsil eder. Yani, Big Oh notasyonu ile Big Omega notasyonu arasında ortalama bir karmaşıklığı ifade eder.

Big O Notasyonu Nedir? Büyük O Gösterimi Nedir?

Big O Notasyonu, algoritma analizindeki zaman karmaşıklığında üst sınırı tanımlayan, matematiksel bir gösterimdir. Algoritmanın büyüme hızını(growth rate) temsil etmek için kullanılır.

Başka bir deyişle, algoritmadaki girdi boyutu büyüdükçe, çalışma süresi veya alan gereksinimlerinin fonksiyondaki asimptotik karşılığını, ifadeleri sadeleştirme yöntemiyle basitleştirerek bulmamızı sağlar.

 Aslında, algoritma analizinin dışında, matematikte de genellikle kırpılmış bir sonsuz serinin kalan terimini karakterize etmek için de kullanılır. İlk olarak Alman sayılar kuramcısı Paul Bachmann tarafından 1892 yılında kullanılmıştır.

Big O Notasyonu ile basit bir şekilde 6n^4 log(n)+12n^4+2n^2+n+24 ifadesini, önce n^4+log n+n^3+n^2+n+1, daha sonra O(n^4 log n) şeklinde gösterebiliriz.

Ya da 4n^2+3n+16 ifadesini, O(n^2) şeklinde gösterebiliriz. Peki bu gösterimleri hangi kurallara göre yapıyoruz?

Büyük O Gösterimi Analiz Kuralları Nelerdir?

Fonksiyonda n’ye bağlı artan değerler için, yine n’ye bağlı şekilde uygulanan bazı kurallar vardır. Bu kuralları aşağıdaki şekilde tanımlayabiliriz. 

f(n), g(n), h(n), ve p(n) pozitif tamsayılar kümesinden, pozitif reel sayılar kümesine tanımlanmış fonksiyonlar olsun:

• Katsayı Kuralı: f(n), O(g(n)) ise o zaman kf(n) yine O(g(n)) olur. Katsayılar önemsizdir.
• Toplam Kuralı: f(n), O(h(n)) ise ve g(n), O(p(n)) verilmişse f(n)+g(n), O(h(n)+p(n)) olur. Üst-sınırlar toplanır.
• Çarpım Kuralı: f(n), O(h(n)) ve g(n), O(p(n)) için f(n)g(n) is O(h(n)p(n)) olur.
• Polinom Kuralı: f(n), k dereceli polinom ise f(n) için O(nk ) kabul edilir.
• Kuvvetin Log’u Kuralı: log(nk ) için O(log(n)) dir.

Bu kuralların dışında, yürütme zamanı başlığında da incelediğimiz birçok örnekle ilişikli olan, algoritmada bulunan kodlara uygulanacak kurallar da vardır. Bu kurallar ise başlıca:

Big O Notasyonu Sabit Algoritma

• Döngüler: Bir döngünün çalışma zamanı döngü sayısının bir c sabitiyle çarpımı kadardır. Ancak, eğer bir döngünün n değeri sabit verilmişse. Örneğin: n = 100 ise değeri O(1)’dir.
• İç-içe döngüler: İçten dışa doğru her döngünün çalışma sayısı dıştaki döngü ile çarpılırken, sabit değerler de çarpıma dahil edilir.
• Ardışık ifadeler: Her bir ifadenin zaman karmaşıklığı eklenerek tek bir fonksiyon elde edilir.
• Logaritmik karmaşıklık: Bir algoritma, problemin çözüm kümesini belli sabit oranında bölüyorsa(örneğin ½ oranında), O(logn) şeklinde gösterilir.

Big-O Notasyonu Avantajları Nelerdir?

Big-Oh notasyonunun belli başlı avantajları vardır. Daha önce de çokça bahsettiğimiz gibi algoritma analizinde derleyici, donanım, bellek hızı gibi bağımlılıklardan dolayı belli bir komutun çalışma süresi farklılık gösterebilir.  Amaç bu etkenlerden bağımsız bir şekilde, algoritmanın verimliliğini ölçmektir. Big O gösterimi ile algoritmadaki sabitler ve diğer gereksiz etmenler göz ardı edilir ve analizi daha da basitleştirir.

Örneğin, 5.4n3 yerine sadece n3 `e odaklanırız. Özetle algoritmalar arasındaki kıyaslamayı, tek bir değere indirgeyerek bizi zahmetten kurtarır.

Şimdi de son olarak Big O gösterimini döngüler bazında inceleyelim.

Big Oh Notasyonu Örnekler

Lineer (Doğrusal) Döngü - Lineer Zaman - O(n)

i = 1
while(i < 100):
	i += 1
	# işlemler

Big O Notasyonu Doğrusal Lineer Algoritma Grafiği

Logaritmik Döngü (Logarithmic) - Logaritmik Zaman - O(log n)

i = 1
while(i < 100):
	i *= 2
	# işlemler

i = 100
while(i >= 1):
	i /= 2
	print(i)
	# işlemler

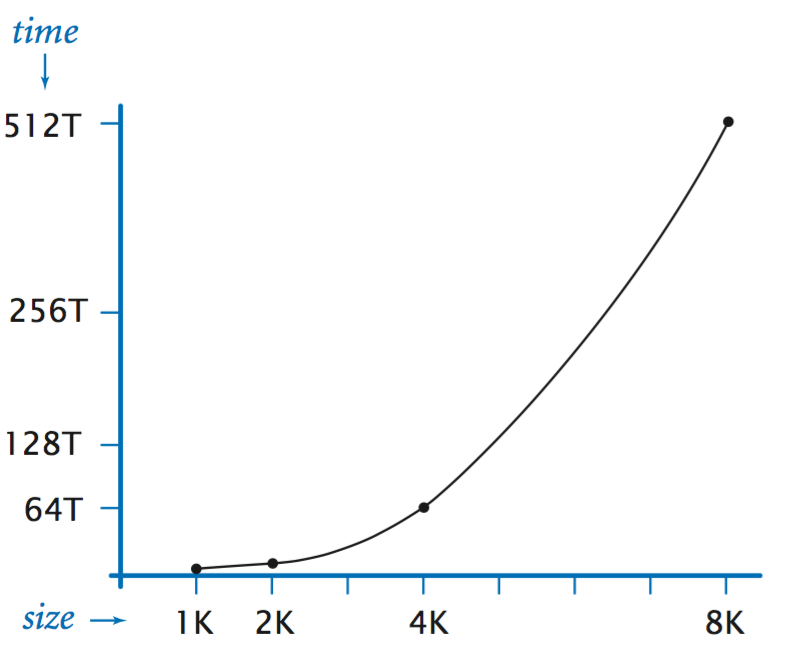
Büyük O Gösterimi Logaritmik Algoritma Örneği

Karesel ve Bağımlı Karesel Döngü - Üstel Zaman - O(n2)

i = 1
while(i <= 10):
	j = 1
	while(j <= 10):
		j += 1
	i += 1

i = 1
while(i <= 100):
	j = 1
	while(j <= i):
		j += 1
	i += 1

Big O Notation Karesel Algoritma (Loop)

Lineer Logaritmik Döngü - O(nlog n)

i = 1
while(i <= 10):
	j = 1
	while(j <= 10):
		j *= 2
	i += 1

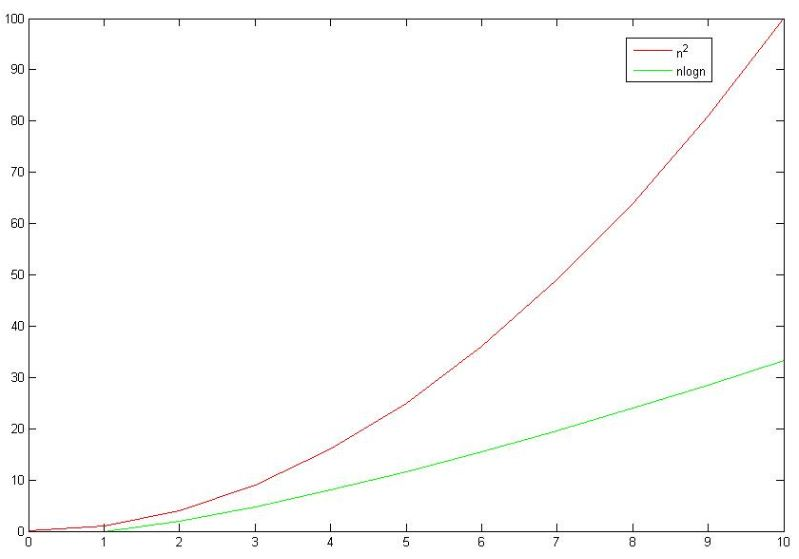
Büyük O Notasyonu Lineer-Logaritmik Algoritma Örneği

SONUÇ

Artık algoritma analizinin nasıl yapıldığını, neden önemli olduğunu, karmaşıklık analizinin nasıl yapıldığını ve büyük o gösteriminin ne olduğunu az çok anladık diye düşünüyorum. Hatalı veya karışık olduğunu düşündüğünüz ya da eksik kaldığını düşündüğünüz noktalar için yorum yapabilirsiniz.